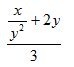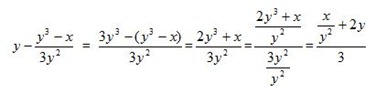一人読書会「計算機プログラムの構造と解釈」 (8)

1.1.7 Newton 法による平方根

問題　1.8

立方根をとるNewton法は y が x の立方根の近似値なら、よりよい近似は以下の値で与えられるという事実によっている。この手続きを実装せよ。

まず、平方根同様に、式を確認。

納得いった。

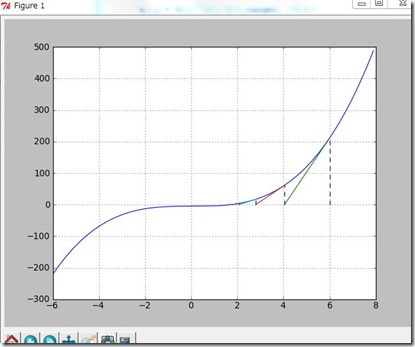
いきなりSchemeでかけるほど訳がわかっていないので、まずは、イメージをつかむために、Python でグラフを書いてみる。5 の立方根を計算。

# -*- encoding:utf-8 -*-
'''
Newton 近似により、平方根を求めるサンプル
'''

from pylab import *
from numpy import *
from numpy.ma.core import arange
from decimal import *

def d(x):
    return Decimal(x)

cube = lambda x, b : d(x) ** d('3') - d(b)         
newton = lambda target, guess : (d(target) / (d(guess) ** d('2')) + (d('2') * d(guess))) / d('3')

def f1(x_range, target, interval):
    x = arange(d(x_range[0]), d(x_range[1]), d(interval))
    y = [cube(y1, target) for y1 in x]

    return (x, y)

if __name__ == '__main__':
    grid(True)
    getcontext().prec = 8
    target = d('5')
    
    # 3次元のグラフ
    x, y = f1(('-6','8'),target, '0.1')
    plot(x,y)

    guess = d('6.0')
    repeat = 8
    for i in range(repeat):
        x = (guess, guess)
        y = (d('0'), cube(guess, target))
        plot(x, y, 'k--')

        new_guess = newton(target, guess)
        
        x = (guess, new_guess)
        y = (cube(guess, target), d('0'))
        plot(x, y)
    
        guess = new_guess
        print guess

    show()